Metrics (모델의 성능 지표)
각각의 지표는 머신 러닝 및 딥러닝 모델의 성능 측정에 사용되는 평가 지표 중 일부입니다.
아래에 각 지표에 대한 공식과 간단한 설명을 제공하겠습니다.
1. Confusion Matrix (혼동 행렬)

- 설명: Confusion Matrix(혼동 행렬)은 이진 분류(binary classification) 모델의 성능을 평가하기 위한 표입니다.
주로 머신러닝과 통계학에서 사용되며, 모델이 예측한 클래스와 실제 클래스 간의 관계 시각화, 평가에 유용 - TP(True Positive): 실제 양성 클래스를 정확하게 예측
- FN(False Negative): 실제 양성 클래스를 음성으로 잘못 예측
- FP(False Positive): 실제 음성 클래스를 양성으로 잘못 예측
- TN(True Negative): 실제 음성 클래스를 정확하게 예측
2. Accuracy (정확도)
- 공식: (True Positives+ True Negatives) / (Total Examples)
- 설명: 전체 예측 중 올바르게 예측한 비율로, 클래스 불균형이 적은 경우에 유용
- 예시: TP=80, TN=120, FP=10, FN=5

from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
# 가상의 데이터 생성
X, y = ... # 독립변수(Feature), 종속변수(Label) 데이터
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# 모델 훈련
model = LogisticRegression()
model.fit(X_train, y_train)
# 예측
y_pred = model.predict(X_test)
# 평가 지표 계산
accuracy = accuracy_score(y_test, y_pred)3. Precision (정밀도)
- 공식: True Positives / (True Positives + False Positives)
- 설명: 모델이 양성으로 예측한 것 중 실제로 양성인 비율로, 거짓 양성(FP)을 최소화하려는 경우에 중요
- 예시: TP=80, TN=120, FP=10, FN=5

from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
# 가상의 데이터 생성
X, y = ... # 독립변수(Feature), 종속변수(Label) 데이터
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# 모델 훈련
model = LogisticRegression()
model.fit(X_train, y_train)
# 예측
y_pred = model.predict(X_test)
# 평가 지표 계산
precision = precision_score(y_test, y_pred)4. Recall (재현율)
- 공식: True Positives / (True Positives + False Negatives)
- 설명: 실제 양성 중 모델이 얼마나 많이 감지했는지를 나타내며, 거짓 음성(FN)을 최소화하려는 경우에 중요
- 예시:TP=80, TN=120, FP=10, FN=5

from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
# 가상의 데이터 생성
X, y = ... # 독립변수(Feature), 종속변수(Label) 데이터
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# 모델 훈련
model = LogisticRegression()
model.fit(X_train, y_train)
# 예측
y_pred = model.predict(X_test)
# 평가 지표 계산
recall = recall_score(y_test, y_pred)5. F1 Score (F1 점수)
- 공식: 2 * (Precision * Recall) / (Precision + Recall)
- 설명: 정밀도와 재현율의 조화 평균으로, 두 지표를 모두 고려할 때 사용되며, 불균형한 클래스 분포에서 유용
- 예시: TP=80, TN=120,FP=10, FN=5 → Precision=0.889, Recall=0.941
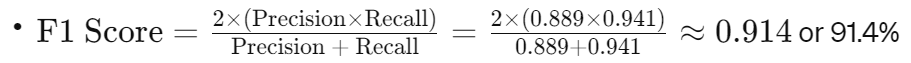
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
# 가상의 데이터 생성
X, y = ... # 독립변수(Feature), 종속변수(Label) 데이터
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# 모델 훈련
model = LogisticRegression()
model.fit(X_train, y_train)
# 예측
y_pred = model.predict(X_test)
# 평가 지표 계산
f1 = f1_score(y_test, y_pred)6. MSE (Mean Squared Error, 평균 제곱 오차)
- 공식: (1/n) * Σ(yᵢ - ŷᵢ)² (for i from 1 to n)
- 설명: 예측값-실제값 간의 차이를 제곱하여 평균한 값으로, 회귀 문제에서 주로 사용
- 장점: 큰 오차에 대해 더 높은 페널티를 부여하므로 모델이 큰 오차를 최소화하도록 유도
- 단점: 오차를 제곱하기 때문에 오류의 크기가 커질수록 더 커지는 경향 (이상치에 민감)
- 예시: 실제값(yᵢ)=[10, 20, 30, 40, 50], 예측값(ŷᵢ)=[12, 18, 35, 42, 55]

from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
# 가상의 데이터 생성
X, y = ... # 독립변수(Feature), 종속변수(Label) 데이터
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 모델 훈련
model = LinearRegression()
model.fit(X_train, y_train)
# 예측
y_pred = model.predict(X_test)
# 평가 지표 계산
mse = mean_squared_error(y_test, y_pred)7. MAE (Mean Absolute Error, 평균 절대 오차)
- 공식: (1/n) * Σ|yᵢ - ŷᵢ| (for i from 1 to n)
- 설명: 예측값-실제값 간의 차이의 절대값를 평균한 값으로, 회귀 문제에서 사용
- 장점: 이상치에 덜 민감하며, 예측값과 실제값의 실제 차이를 반영
- 단점: 오차에 대해 선형적으로 평가하므로, 큰 오차에 대한 뚜렷한 페널티 X
- 예시: 실제값(yᵢ)=[10, 20, 30, 40, 50], 예측값(ŷᵢ)=[12, 18, 35, 42, 55]

from sklearn.metrics import mean_absolute_error
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
# 가상의 데이터 생성
X, y = ... # 독립변수(Feature), 종속변수(Label) 데이터
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 모델 훈련
model = LinearRegression()
model.fit(X_train, y_train)
# 예측
y_pred = model.predict(X_test)
# 평가 지표 계산
mae = mean_absolute_error(y_test, y_pred)8. RMSE (Root Mean Squared Error, 평균 제곱근 오차)
- 공식: √((1/n) * Σ(yᵢ - ŷᵢ)²) (for i from 1 to n)
- 설명: MSE의 제곱근으로, 예측값-실제값 간의 표준편차(예측 오차의 평균 크기) 값으로, 회귀 문제에서 사용
- 장점: MSE의 단점인 오차 크기의 제곱을 보완하면서, 오차의 크기에 대해 직관적인 해석을 제공
- 단점: 오차가 크면 클수록 페널티가 급격하게 증가 (이상치에 민감)
- 예시: 실제값(yᵢ)=[10, 20, 30, 40, 50], 예측값(ŷᵢ)=[12, 18, 35, 42, 55], MSE=12.4

from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
import numpy as np
# 가상의 데이터 생성
X, y = ... # 독립변수(Feature), 종속변수(Label) 데이터
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 모델 훈련
model = LinearRegression()
model.fit(X_train, y_train)
# 예측
y_pred = model.predict(X_test)
# 평가 지표 계산
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse)9. MAPE (Mean Absolute Percentage Error, 평균 절대 백분 오차)
- 공식: ((100/n) * Σ|(Aᵢ - Fᵢ)/Aᵢ| (for i from 1 to n)
- 설명: 실제값-예측값의 백분율 오차의 평균으로,
주로 예측 모델이 시계열 데이터나 금융 데이터와 같은 연속적인 값을 예측하는 경우에 사용 - 장점: 백분율 오차를 측정하여 예측의 상대적인 정확성을 직관적으로 이해할 수 있습니다.
여러 예측 모델 간의 성능을 비교하기 용이합니다. - 단점: 오차의 백분율을 계산하므로 실제값이 0에 가까운 경우 오류가 발생할 수 있습니다.
예측값과 실제값이 0인 경우에는 MAPE 계산 X

from sklearn.linear_model import LinearRegression
import numpy as np
# 가상 데이터 생성
np.random.seed(0)
X = np.random.rand(100, 1) * 10
y = 2 * X.squeeze() + np.random.normal(scale=2, size=100)
# 모델 훈련
model = LinearRegression()
model.fit(X, y)
# 예측
y_pred = model.predict(X)
# 평가 지표 계산
def mape(y_true, y_pred):
return np.mean(np.abs((y_true - y_pred) / y_true)) * 100
mape_score = mape(y, y_pred)10. ROC-AUC
- 설명: 이진 분류 모델의 성능을 평가하는 지표 중 하나로, ROC 곡선의 아래 면적을 측정한 값
일반적으로 0~1 사이의 값을 가집니다. 완벽한 분류 모델의 경우 AUC=1, 무작위 분류 모델의 경우 AUC=0.5 - 장점: 클래스 간 샘플 수가 크게 다른 불균형한 클래스 분포에서도 신뢰할 수 있는 성능 평가 지표로 사용 가능
- 단점: 클래스 불균형이 심한 데이터셋에서는 모델의 성능을 왜곡할 수 있습니다.
클래스 분포가 변경되어도 변하지 않아 실제 비즈니스 상황과의 일치를 제대로 반영하지 못할 수 있습니다.
from sklearn.metrics import roc_auc_score
# 실제 값
y_true = [0, 0, 1, 1]
# 모델의 예측 확률
y_scores = [0.1, 0.4, 0.35, 0.8]
# 평가 지표 계산
roc_auc = roc_auc_score(y_true, y_scores)
ROC AUC: 0.75
본 게시글은 ChatGPT의 도움을 받아 작성하였습니다.
'AI > Machine Learning' 카테고리의 다른 글
| 분류 모델 / 회귀 모델 (0) | 2024.01.17 |
|---|---|
| Ensemble (앙상블) (0) | 2024.01.10 |
| 다중공선성 (VIF, 분산팽창계수) (0) | 2023.12.18 |
| 라벨 인코딩, 원핫 인코딩 (0) | 2023.11.10 |
| K-fold 교차 검증 (2) | 2023.10.29 |



